技术数据结构算法cpp链式二叉树的遍历、节点个数和单值二叉树问题
chenlei@TOC

前言
- 链式二叉树增删查改的价值
- 堆的意义:插入数据的意义—排序、topk
- 普通链式二叉树没有意义
- 我们学习当前链式二叉树有以下两目的
- 更复杂的二叉搜索树->AVL 红黑树(以后打基础)——高阶
- 排序二叉树
- 搜索二叉树——左边比根小,右边比根大
- 很多二叉树的题是在这一块(笔试面试O阶题)
- 所以二叉树这块的重点不是增删查改,而是学习二叉树的结构,为之后学习打基础。
定义结构—BinaryTreeNode
1
2
3
4
5
6
7
8
| typedef int BTDataType;
typedef struct BinaryrTreeNode
{
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
BTDataType val;
}BTNode;
|
手动构建—BuyNode
构建如下树:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| BTNode* BuyTreeNode(BTDataType x)
{
BTNode* node = (BTNode*)malloc(sizeof(BTNode));
if (node == NULL)
{
perror("malloc error\n");
exit(-1);
}
node->val = x;
node->left = NULL;
node->right = NULL;
return node;
}
int main()
{
BTNode* node1 = BuyTreeNode(1);
BTNode* node2 = BuyTreeNode(2);
BTNode* node3 = BuyTreeNode(3);
BTNode* node4 = BuyTreeNode(4);
BTNode* node5 = BuyTreeNode(5);
BTNode* node6 = BuyTreeNode(6);
node1->left = node2;
node1->right = node4;
node2->left = node3;
node4->left = node5;
node4->right = node6;
}
|
三种遍历
前序遍历 PrevOrder
1
2
3
4
5
6
7
8
9
10
11
12
| void PreOrder(BTNode* node)
{
if (node == NULL)
{
printf("NULL ");
return;
}
printf("%d ", node->val);
PreOrder(node->left);
PreOrder(node->right)
}
|
中序遍历 InOrder
1
2
3
4
5
6
7
8
9
10
| void InOrder(BTNode* node)
{
if (node == NULL)
{
return;
}
InOrder(node->left);
printf("%d ", node->val);
PreOrder(node->right);
}
|
后序遍历 PostlOrder 同理可得
1
2
3
4
5
6
7
8
9
10
| void PostOrder(BTNode* node)
{
if (node == NULL)
{
return;
}
InOrder(node->left);
PreOrder(node->right);
printf("%d ", node->val);
}
|
图示(中序为例)

为了更好理解其中过程我画了如下函数图(以中序为例):

如图得到中序的结果;
每个函数调用都建立一个栈帧:
【注意:空内存也调用栈帧】
结束后销毁回到调用处
调用栈帧
递归展开图画到NULL后回调
如何求树中节点个数
节点个数
一般方法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
int size = 0;
int treesize(btnode* root)
{
if (root == null)
return;
else
size++;
treesize(root->left);
size = 0;
treesize(root->right);
return size;
}
|
牛逼方法(递归思路)
1
2
3
4
5
6
7
8
9
10
11
| int TreeSize(BTNode* root)
{
if (root == NULL)
return 0;
else
return TreeSize(root->left)
+ TreeSize(root->right)+1;
}
|
在返回时先求左子树在求右子树最后求自己,所以本质是求其后序。
叶子节点个数
”分而治之“的思想
是叶子的条件:左右节点为NULL
- 判断左右节点是否为NULL,其后将叶子节点相加
- 左右都为NULL,返回1
- 左子树+右子树
1
2
3
4
5
6
7
8
9
10
11
|
int TreeLeaveSize(BTNode* root)
{
if (root == NULL)
return 0;
if (root->left == NULL && root->right == NULL)
return 1;
return TreeLeaveSize(root->left)
+ TreeLeaveSize(root->right);
}
|
第k层节点个数
假设求第三层——>求第二层的子树的节点个数——>第一层的子树的节点个数
- k层=左子树k-1层 + 右子树k-1层(作为递进条件)
->> 访问到空节点返回0;(作为回归条件)
->> 访问到节点。
1
2
3
4
5
6
7
8
9
10
|
int TreeKLevel(BTNode* root ,int k)
{
if (root == NULL)
return 0;
if (root != NULL)
return 1;
return TreeKLevel(root->left, k - 1)
+ TreeKLevel(root->right, k - 1);
}
|
将问题化为最小子问题。
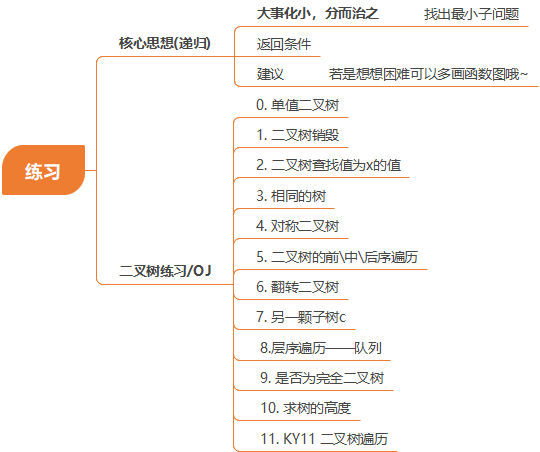
练习
单值二叉树

递进条件
左子树
回归条件
- ture
左/右子树为NULL
左右子树和根相等
- false
左子树不等于根
右子树不等于根
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
bool isUnivalTree(struct TreeNode* root){
if(root==NULL)
return true;
if(root->left && root->left->val != root->val)
return false;
if(root->right && root->right->val != root->val)
return false;
return isUnivalTree(root->left)
&&isUnivalTree(root->right);
}
|
今日份总代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
| #define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<stdlib.h>
typedef int BTDataType;
typedef struct BinaryrTreeNode
{
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
BTDataType val;
}BTNode;
BTNode* BuyTreeNode(BTDataType x)
{
BTNode* node = (BTNode*)malloc(sizeof(BTNode));
if (node == NULL)
{
perror("malloc error\n");
exit(-1);
}
node->val = x;
node->left = NULL;
node->right = NULL;
return node;
}
void PreOrder(BTNode* node)
{
if (node == NULL)
{
printf("NULL ");
return;
}
printf("%d ", node->val);
PreOrder(node->left);
PreOrder(node->right);
}
void InOrder(BTNode* node)
{
if (node == NULL)
{
printf("NULL ");
return;
}
InOrder(node->left);
printf("%d ", node->val);
PreOrder(node->right);
}
void PostOrder(BTNode* node)
{
if (node == NULL)
{
printf("NULL ");
return;
}
InOrder(node->left);
PreOrder(node->right);
printf("%d ", node->val);
}
int TreeSize(BTNode* root)
{
return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}
int TreeLeaveSize(BTNode* root)
{
if (root == NULL)
return 0;
if (root->left == NULL && root->right == NULL)
return 1;
return TreeLeaveSize(root->left) + TreeLeaveSize(root->right);
}
int TreeKLevel(BTNode* root ,int k)
{
if (root == NULL)
return 0;
if (root != NULL)
return 1;
return TreeKLevel(root->left, k - 1) + TreeKLevel(root->right, k - 1);
}
int main()
{
BTNode* node1 = BuyTreeNode(1);
BTNode* node2 = BuyTreeNode(2);
BTNode* node3 = BuyTreeNode(3);
BTNode* node4 = BuyTreeNode(4);
BTNode* node5 = BuyTreeNode(5);
BTNode* node6 = BuyTreeNode(6);
node1->left = node2;
node1->right = node4;
node2->left = node3;
node4->left = node5;
node4->right = node6;
PreOrder(node1);
printf("\n");
InOrder(node1);
printf("\n");
PostOrder(node1);
printf("\n");
printf("%d\n", TreeSize(node1));
printf("%d\n", TreeSize(node1));
printf("%d\n", TreeLeaveSize(node1));
return 0;
}
|
感谢各位老铁能看到这里,还请给个免费的赞哦~❤️❤️❤️❤️❤️